La capacidad calorífica específica, calor específico o capacidad térmica específica es una magnitud física que se define como la cantidad de calor que hay que suministrar a la unidad de masa de una sustancia o sistema termodinámico para elevar su temperatura en una unidad. En general, el valor del calor específico depende del valor de la temperatura inicial. Se le representa con la letra  (minúscula).
(minúscula).
 (minúscula).
(minúscula).
De forma análoga, se define la capacidad calorífica como la cantidad de calor que hay que suministrar a toda la masa de una sustancia para elevar su temperatura en una unidad (kelvin o grado Celsius). Se la representa con la letra 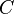 (mayúscula).
(mayúscula).
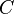 (mayúscula).
(mayúscula).
Por lo tanto, la capacidad calorífica específica es el cociente entre la capacidad calorífica y la masa, esto es 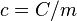 donde
donde 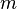 es la masa de la sustancia.
es la masa de la sustancia.
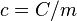 donde
donde 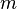 es la masa de la sustancia.
es la masa de la sustancia.
 ) correspondiente a un cierto intervalo de temperaturas
) correspondiente a un cierto intervalo de temperaturas  se define en la forma:
se define en la forma:
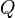 es la transferencia de energía en forma calorífica entre el sistema y su entorno u otro sistema,
es la transferencia de energía en forma calorífica entre el sistema y su entorno u otro sistema,  es la masa del sistema (se usa una n cuando se trata del calor específico
es la masa del sistema (se usa una n cuando se trata del calor específico 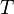 se define como:
se define como:
 . Esta función es creciente para la mayoría de las sustancias (excepto para los gases
. Esta función es creciente para la mayoría de las sustancias (excepto para los gases  a la final
a la final  se calcula mediante la integral siguiente:
se calcula mediante la integral siguiente:
