La capacidad calorífica específica media (
) correspondiente a un cierto intervalo de temperaturas 
se define en la forma:
) correspondiente a un cierto intervalo de temperaturas se define en la forma:
donde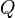 
es la transferencia de energía en forma calorífica entre el sistema y su entorno u otro sistema, 
es la masa del sistema (se usa una n cuando se trata del calor específico molar) y es el incremento de temperatura que experimenta el sistema. El calor específico (
) correspondiente a una temperatura dada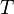 
se define como:
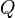es la transferencia de energía en forma calorífica entre el sistema y su entorno u otro sistema, es la masa del sistema (se usa una n cuando se trata del calor específico molar) y es el incremento de temperatura que experimenta el sistema. El calor específico () correspondiente a una temperatura dada 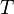se define como:
La capacidad calorífica específica () es una función de la temperatura del sistema; esto es, 
. Esta función es creciente para la mayoría de las sustancias (excepto para los gases monoatómicos y diatómicos). Esto se debe a efectos cuánticos que hacen que los modos de vibración estén cuantizados y solo estén accesibles a medida que aumenta la temperatura. Conocida la función , la cantidad de calor asociada con un cambio de temperatura del sistema desde la temperatura inicial 
a la final 
se calcula mediante la integral siguiente:
) es una función de la temperatura del sistema; esto es, . Esta función es creciente para la mayoría de las sustancias (excepto para los gases monoatómicos y diatómicos). Esto se debe a efectos cuánticos que hacen que los modos de vibración estén cuantizados y solo estén accesibles a medida que aumenta la temperatura. Conocida la función , la cantidad de calor asociada con un cambio de temperatura del sistema desde la temperatura inicial a la final se calcula mediante la integral siguiente:
En un intervalo donde la capacidad calorífica sea aproximadamente constante la fórmula anterior puede escribirse simplemente como:
No hay comentarios:
Publicar un comentario